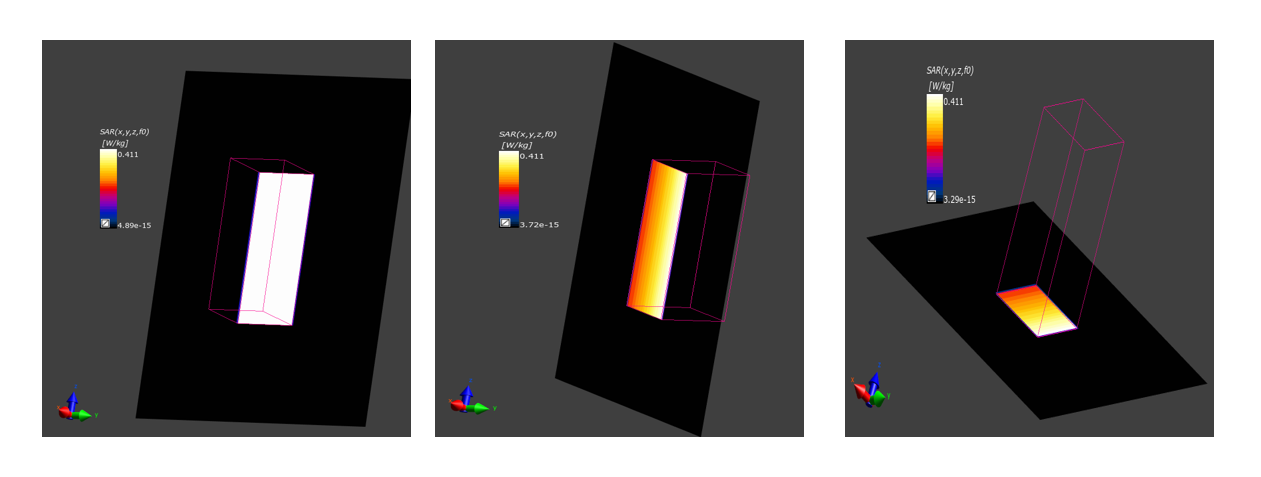
Homogeneity of E-filed map in plane wave simulation

[Sylvain]

If there is a gel, I would expect it is dissipating some power (just check the SAR, for instance...). In that case, you should expect the E field to decrease in intensity in the direction of propagation.

[Saya]

I'm wondering why energy dissipation does not happen in z-direction (since in yz plane E-field is homogeneous)?

[Saya]

@Saya

[Saya]

I ran the simulation with a finer grid and for a longer time, but the result is still the same.

[Sylvain]

@Saya said in Homogeneity of E-filed map in plane wave simulation:

I'm wondering why energy dissipation does not happen in z-direction (since in yz plane E-field is homogeneous)?

Because your wave is propagating in the X direction.

Your simulation results make perfect sense: a wave is propagating through a lossy medium, dissipating some energy in the process.

[Saya]

So you mean in the simulation with gel, because of the power loss in x direction, E-field should be non homogeneous in xz and xy planes.
I checked the simulation without gel(with just air) and it seems E-field is homogeneous in all planes. Great. Thanks.
And two more questions,

• Why in the tutorial, the air is considered as gel and gel is not used as an object in the simulation?
• Where is the starting point of the wave propagation?
  Thanks.

[Sylvain]

• The "air" is not considered as "gel". Rather, the background material, which is by default "air", is set to "gel" instead. The background is not an object itself: it is the space that is not occupied by any object. As such, it does not have an explicit shape, but it has material properties.
• For a plane wave source, the E and H fields are imposed (based on the analytical expression of a plane wave) on the face(s) "upwind" from the direction of propagation. Note that this is an idealized concept, as true plane waves don't exist in nature (https://en.wikipedia.org/wiki/Plane_wave)

[Saya]

Thanks for your explanation. But I'm still wondering why the background is set to gel? Why the gel is not used as an object?

[Sylvain]

I'm not sure. Maybe because you would then have to consider the size and shape of said object, its interface with the "background", possible intersection with the sides of the computational domain (which the plane wave source may not allow), etc... All of that for zero benefit, since the medium of propagation is a gel, not air or vaccuum.

[Saya]

Right. Thank you very much for your explanation and comments.