The SAR values are greatly different for the Gaussian and sine waveforms
-
When I choose the sine wave which has the frequency of 835MHz and ampitude of 100V as the excitation signal, the computed SAR value is about the 411 W/kg. However, when I only change the excitation signal into the Gaussian waveform which has the center frequency of 835MHz, the bandwidth of 835MHz and the amplitude of 100V/m, the computed SAR value is about 1×10(-15) which is much smaller than the result computed by the sine wave. I want to know the reason. Thank you guys
-
You need to make sure that the SAR is normalized with respect to the same quantity (e.g., input power or conducted power) and target value in both cases.
@ofli Thank you. I have checked that I didn't select the nomalization. When I check the normalization, the value is almost the same for the two excitation waveforms. However, I just wonder why we should select the option of normalization. I mean the real value should be computed directly by the sim4life. Why we must use the normalization? If we select the normalization, I guess the real value of the SAR = normalized factore × computed SAR. I don't know wheter I think is right. I cannot find the answer in the help demo. Could you please explain this to me?
-
Please refer to "Power Balance" section (under EM FDTD Theory) of Sim4Life Manual. And please check voltage & current (and input power) at the source sensor in your Harmonic and Gaussian simulations. As you will see, you are exciting the system (check Sources section in the manual) at different power levels thus if you want to compare harmonic and gaussian cases, you need to normalize in both cases to the same input power. I don't know what you mean by real value of SAR.
-
Please refer to "Power Balance" section (under EM FDTD Theory) of Sim4Life Manual. And please check voltage & current (and input power) at the source sensor in your Harmonic and Gaussian simulations. As you will see, you are exciting the system (check Sources section in the manual) at different power levels thus if you want to compare harmonic and gaussian cases, you need to normalize in both cases to the same input power. I don't know what you mean by real value of SAR.
@ofli In the simulation, I have set the normalized factor as 1 W. If I have an input voltage of 200V, the corresponding power should be much larger than 1 W. I mean in this situation if I still need to normalization the power factor to 1 W even though the real input power is much larger than 1 W. What the real SAR with the input power not the value of 1 W? Thank you.
-
Please refer to "Power Balance" section (under EM FDTD Theory) of Sim4Life Manual. And please check voltage & current (and input power) at the source sensor in your Harmonic and Gaussian simulations. As you will see, you are exciting the system (check Sources section in the manual) at different power levels thus if you want to compare harmonic and gaussian cases, you need to normalize in both cases to the same input power. I don't know what you mean by real value of SAR.
@ofli Before normalization, the SAR value computed by the Gaussian wave is 3.327e(-16) W/kg.
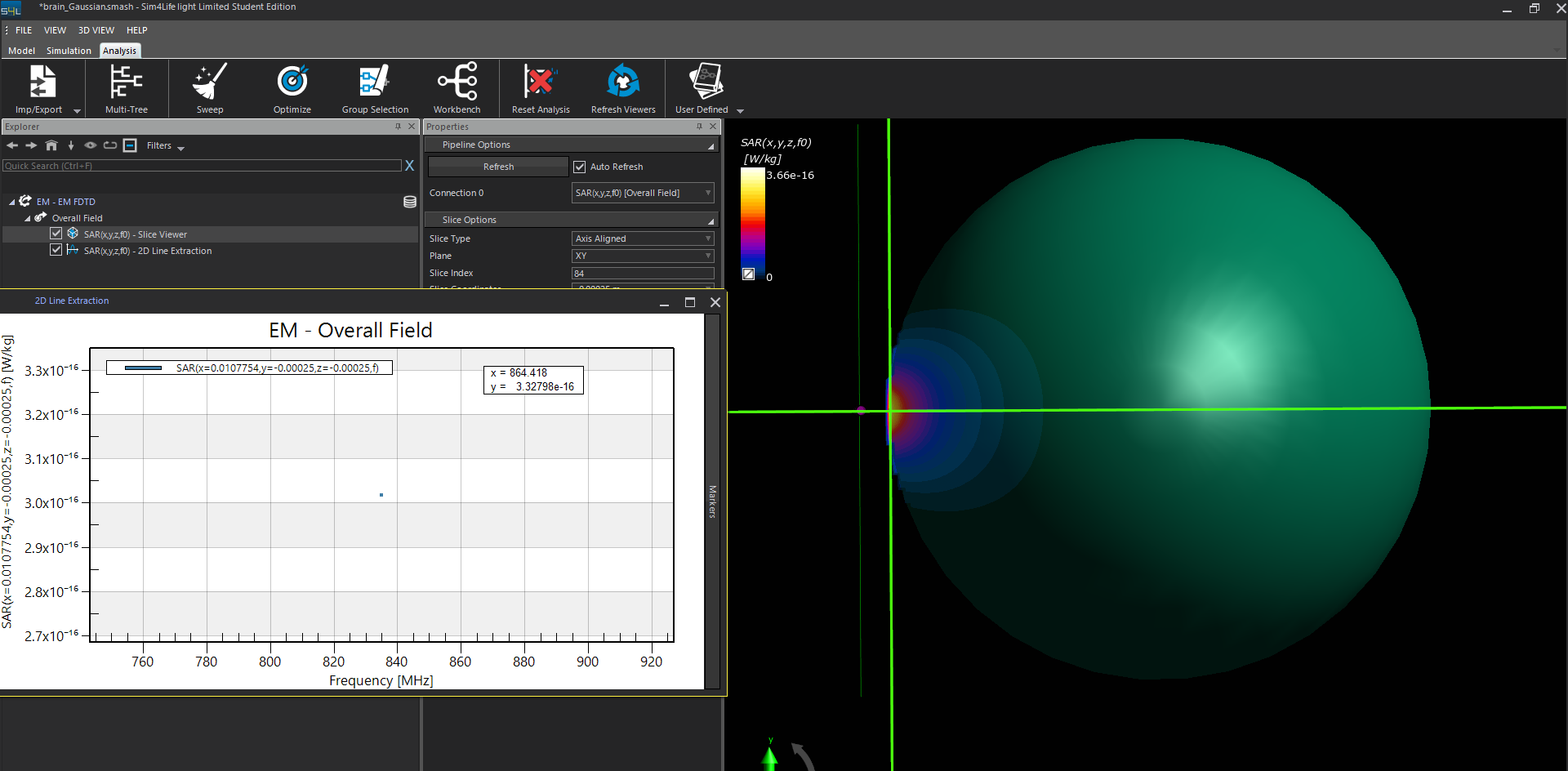
After normalization to 1 W, the SAR value computed by the Gaussian wave reachs about 17.5 W/.
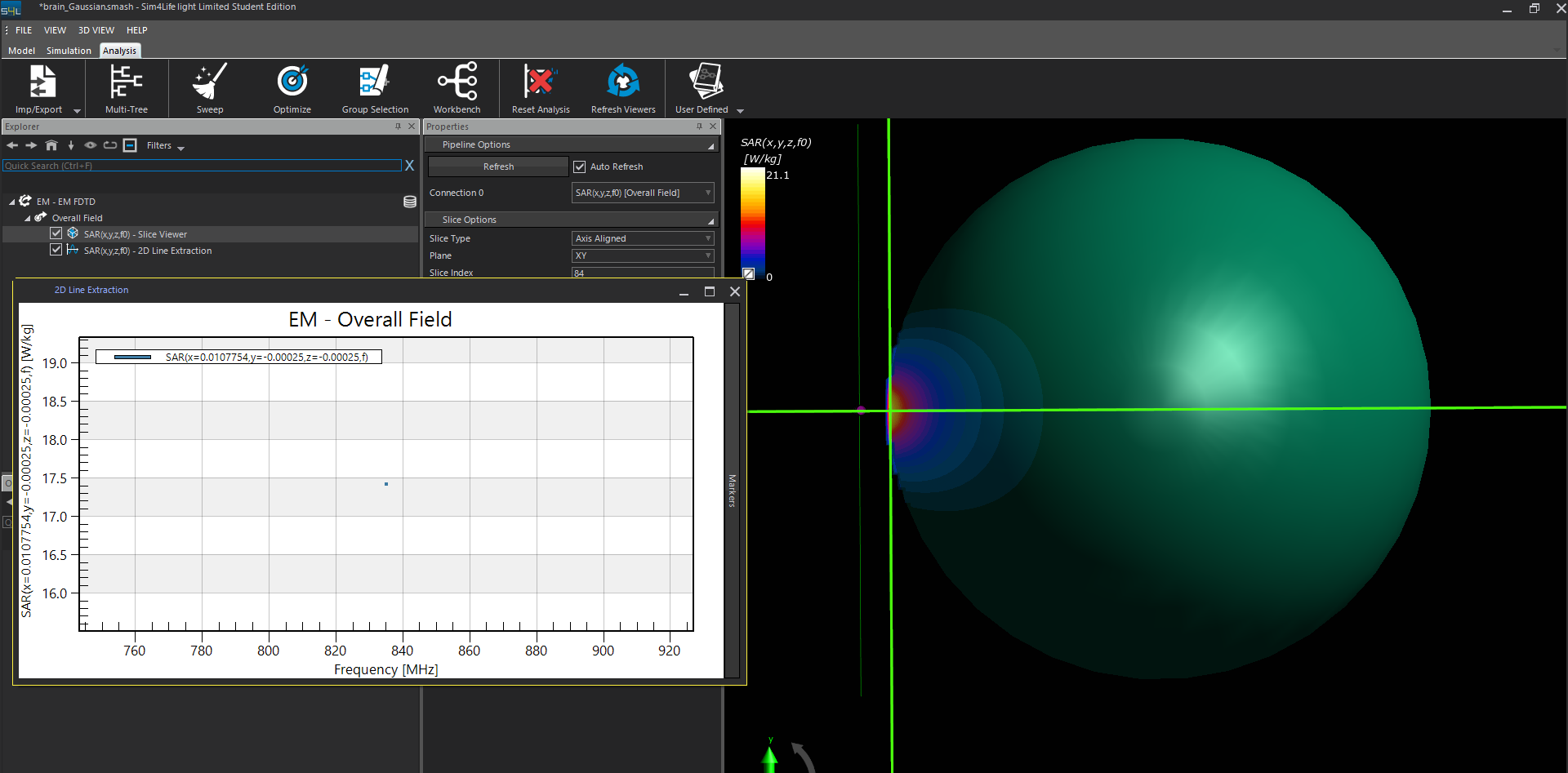
Before normalization, the SAR value computed by the Harmonic wave is 410 W/kg.
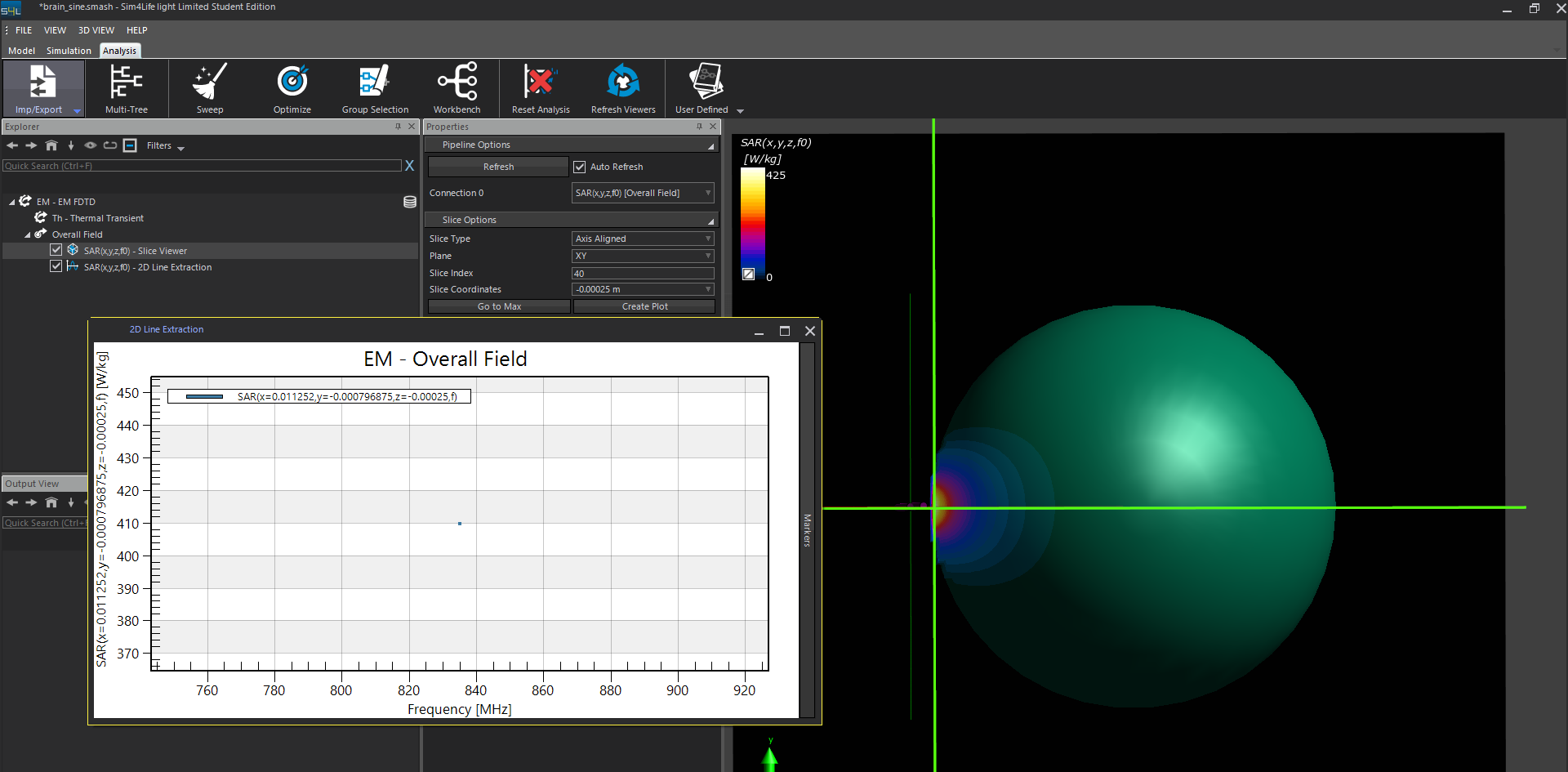
After normalization to 1 W, the SAR value computed by the Harmonic wave is about 16.5 W/kg.
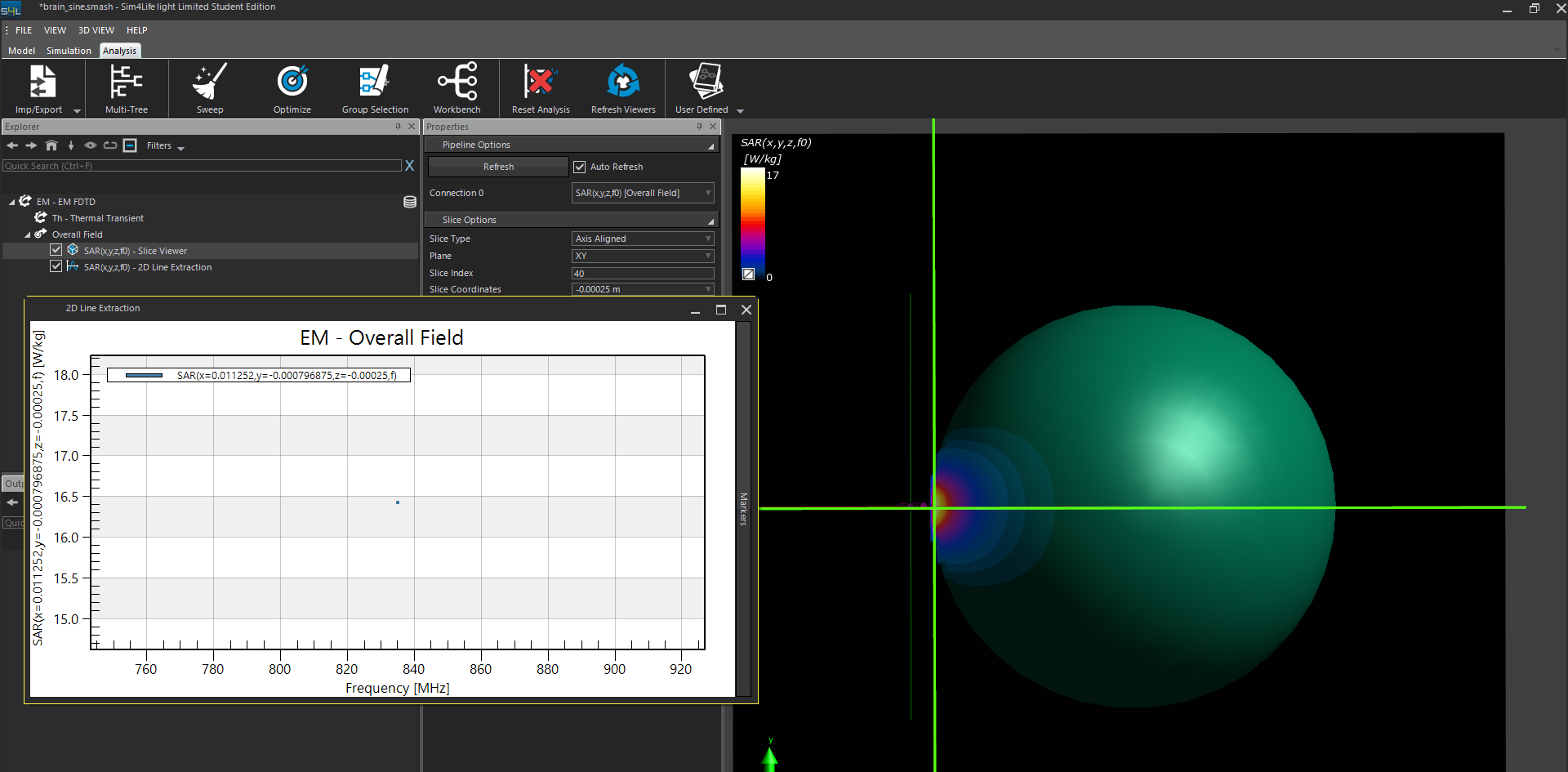
I want to know why the computed results have big difference from each other. Which one should I believe as the real value when the power of the excitation signal is much larger than 1 W? -
@ofli In the simulation, I have set the normalized factor as 1 W. If I have an input voltage of 200V, the corresponding power should be much larger than 1 W. I mean in this situation if I still need to normalization the power factor to 1 W even though the real input power is much larger than 1 W. What the real SAR with the input power not the value of 1 W? Thank you.
@Warren said in The SAR values are greatly different for the Gaussian and sine waveforms:
@ofli In the simulation, I have set the normalized factor as 1 W. If I have an input voltage of 200V, the corresponding power should be much larger than 1 W.
This is where you are probably mistaken: power is voltage times intensity and you don't know what the intensity is. You can actually visualize those quantities, P(t), U(t), I(t), P(f), U(f), I(f), if you look at the output of the edge-sensor in the Analysis tab.
Note that the relationship between voltage U and intensity I is not known a-priori, as it depends on the whole system. For a fixed voltage, the intensity (and hence the power) is only known once the simulation is completed. This is why one cannot set both U and I (or P) as input, and why normalization is the way to go. -
@Warren said in The SAR values are greatly different for the Gaussian and sine waveforms:
@ofli In the simulation, I have set the normalized factor as 1 W. If I have an input voltage of 200V, the corresponding power should be much larger than 1 W.
This is where you are probably mistaken: power is voltage times intensity and you don't know what the intensity is. You can actually visualize those quantities, P(t), U(t), I(t), P(f), U(f), I(f), if you look at the output of the edge-sensor in the Analysis tab.
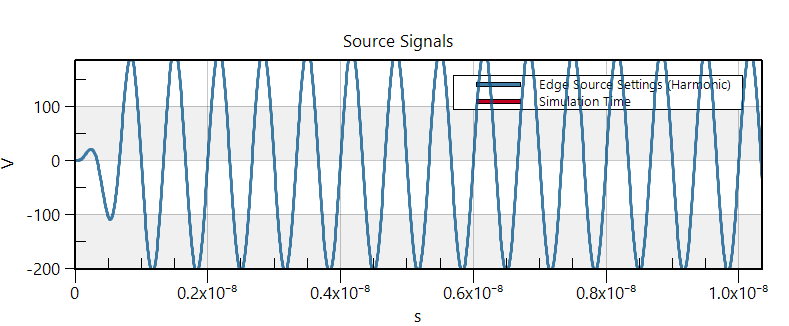
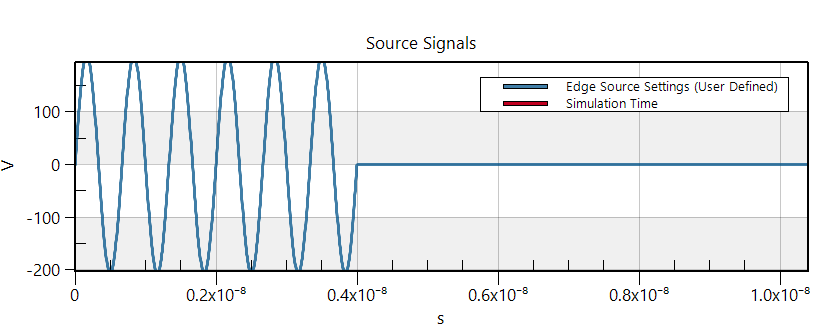
Note that the relationship between voltage U and intensity I is not known a-priori, as it depends on the whole system. For a fixed voltage, the intensity (and hence the power) is only known once the simulation is completed. This is why one cannot set both U and I (or P) as input, and why normalization is the way to go.@Sylvain Thank you for you reply. I think I have known the explaination. Actually, I want use the EM FDTD and the Thermal Transient modules to simulate the heating problem. Firstly, I used the sine waveform as the excitation signal. The microwave induced heat caused significant temperature increasing. However, when I replaced the continuous sine waveform into the waveform with pulse width modulation (the duty cycle is 10%), it doesn't see temperature increasing any more. I noticed that I didn't select the option of normalization in the source of Thermal Transient. I don't knwo whether I should select the normalization and set the scale factor as 1 W? The normal sine waveform and the modulated sine waveform are shown in below, respectively.